General Sparse Constraints

ParOpt now supports general sparse constraints. This new feature is still being developed, but will eventually work in parallel in the same manner as the Jacobian-free sparse constraints in earlier versions of ParOpt. For now these constraints must be for serial problems only.

The following example illustrates the use of sparse constraints on a simple problem. This is the electron problem from the COPS optimization problem set.

To use the sparse constraints, the problem class must still inherit from ParOpt.Problem, but requires different initializer options.

# The super class initialization
super(Electron, self).__init__(
    self.comm,
    nvars=self.nvars,
    num_sparse_constraints=self.num_sparse_constraints,
    num_sparse_inequalities=0,
    rowp=rowp,
    cols=cols,
)

The super class takes the following arguments:

comm The MPI communicator
nvars The number of local variables
num_sparse_constraints The number of sparse constraints
num_sparse_inequalities The number of sparse inequalities - ordered before the equality constraints num_sparse_inequalities <= num_sparse_constraints
rowp An array of length num_sparse_constraints + 1 with the offset into the rows of the sparse constraint Jacobian
cols An array of length rowp[num_sparse_constraints + 1] with the column indices of the variables for each constraint

The member function evalSparseObjCon(self, x, sparse_cons) evaluates the objective, dense constraints and sparse constraints. The sparse constraint values are written directly into sparse_cons that is a direct wrapper into the underlying ParOpt.Vec memory.

The member function evalSparseObjConGradient(self, x, g, A, data) evaluates the objective gradient, dense constraint Jacobian and sparse constraint Jacobian. The sparse constraint Jacobian is written directly into data that is a direct wrapper for the underlying memory of the sparse constraint Jacobian.

[2]:

from paropt import ParOpt, plot_history
import mpi4py.MPI as MPI
import numpy as np
import matplotlib.pylab as plt


class Electron(ParOpt.Problem):
    def __init__(self, n, epsilon):
        # Set the communicator pointer
        self.comm = MPI.COMM_WORLD
        self.n = n
        self.nvars = 3 * n
        self.num_sparse_constraints = n
        self.epsilon = epsilon

        rowp = [0]
        cols = []
        for i in range(self.n):
            cols.extend([i, n + i, 2 * n + i])
            rowp.append(len(cols))

        # Initialize the base class
        super(Electron, self).__init__(
            self.comm,
            nvars=self.nvars,
            num_sparse_constraints=self.num_sparse_constraints,
            num_sparse_inequalities=0,
            rowp=rowp,
            cols=cols,
        )

        return

    def getVarsAndBounds(self, x, lb, ub):
        """Set the values of the bounds"""
        n = self.n

        # x = [x_1, ..., x_n, y_1, ..., y_n, z_1, ..., z_n]
        np.random.seed(0)
        alpha = np.random.uniform(low=0.0, high=2 * np.pi, size=n)
        beta = np.random.uniform(low=-np.pi, high=np.pi, size=n)
        for i in range(n):
            x[i] = np.cos(beta[i]) * np.cos(alpha[i])
            x[n + i] = np.cos(beta[i]) * np.sin(alpha[i])
            x[2 * n + i] = np.sin(beta[i])

        lb[:] = -10.0
        ub[:] = 10.0

        return

    def evalSparseObjCon(self, x, sparse_cons):
        """Evaluate the objective and constraint"""
        n = self.n
        epsilon = self.epsilon
        _x = x[:n]
        _y = x[n : 2 * n]
        _z = x[2 * n :]

        fobj = 0.0
        for i in range(n - 2):
            for j in range(i + 1, n - 1):
                dsq = (_x[i] - _x[j]) ** 2 + (_y[i] - _y[j]) ** 2 + (_z[i] - _z[j]) ** 2
                if dsq < epsilon:
                    dsq = epsilon
                fobj += dsq ** (-1 / 2)

        for i in range(n):
            sparse_cons[i] = 1.0 - (_x[i] ** 2 + _y[i] ** 2 + _z[i] ** 2)

        con = []
        fail = 0

        return fail, fobj, con

    def evalSparseObjConGradient(self, x, g, A, data):
        """Evaluate the objective and constraint gradient"""
        n = self.n
        epsilon = self.epsilon
        _x = x[:n]
        _y = x[n : 2 * n]
        _z = x[2 * n :]

        g[:] = 0.0
        for i in range(n - 2):
            for j in range(i + 1, n - 1):
                dsq = (_x[i] - _x[j]) ** 2 + (_y[i] - _y[j]) ** 2 + (_z[i] - _z[j]) ** 2
                if dsq < epsilon:
                    dsq = epsilon
                else:
                    fact = dsq ** (-3 / 2)
                    g[i] += -(_x[i] - _x[j]) * fact
                    g[j] += (_x[i] - _x[j]) * fact
                    g[n + i] += -(_y[i] - _y[j]) * fact
                    g[n + j] += (_y[i] - _y[j]) * fact
                    g[2 * n + i] += -(_z[i] - _z[j]) * fact
                    g[2 * n + j] += (_z[i] - _z[j]) * fact

        for i in range(n):
            data[3 * i] = -2.0 * _x[i]
            data[3 * i + 1] = -2.0 * _y[i]
            data[3 * i + 2] = -2.0 * _z[i]

        fail = 0

        return fail

# use interior point algorithm
options = {
    "algorithm": "ip",
    "norm_type": "infinity",
    "qn_type": "bfgs",
    "qn_subspace_size": 10,
    "starting_point_strategy": "least_squares_multipliers",
    "qn_update_type": "damped_update",
    "abs_res_tol": 1e-6,
    "barrier_strategy": "monotone",
    "armijo_constant": 1e-5,
    "penalty_gamma": 100.0,
    "max_major_iters": 500,
}

n = 10
problem = Electron(n, 1e-15)
# It is a good idea to check gradients, but this call doesn't work for the moment for sparse constraints
# problem.checkGradients()
opt = ParOpt.Optimizer(problem, options)
opt.optimize()

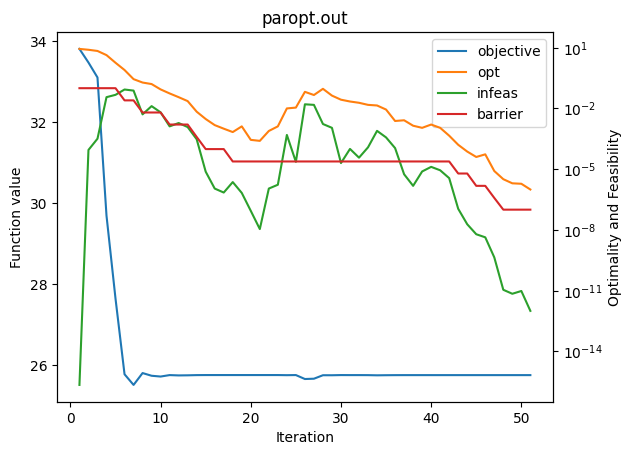
plot_history("paropt.out")

[ ]: